Computer Organization Note (Part 1 of 4)
Part I 包含第一、三章,涉及导论内容和计算机运算问题。
Chapter 1. Computer Abstractions and Technology
History & Development
- 第一代:电子管 / 真空管
- 第二代:晶体管
- 第三代:集成电路
- 第四代:微处理器
Computer Organization
-
Hardware
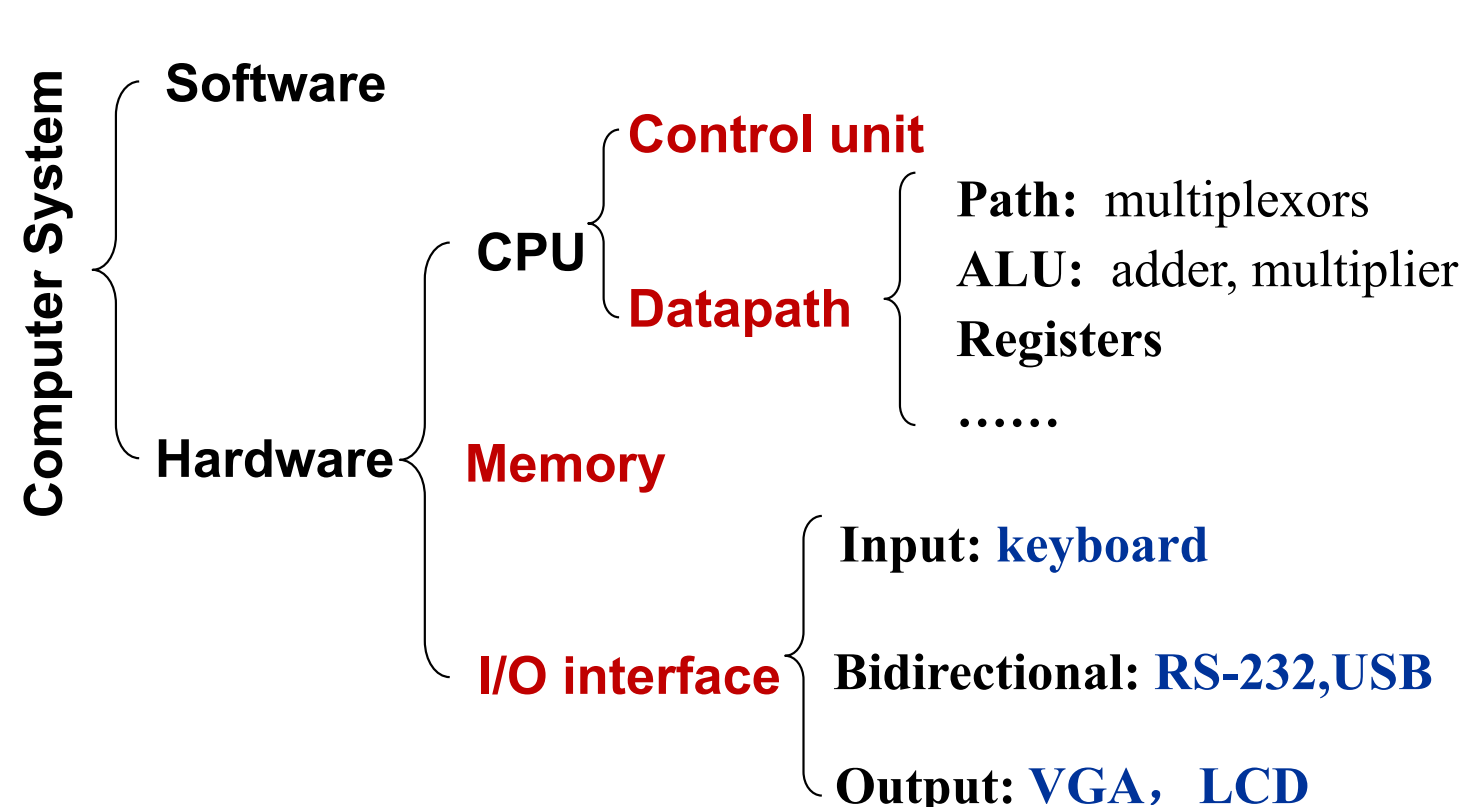
Datapath 可以理解为一条「流水线」。
-
Software
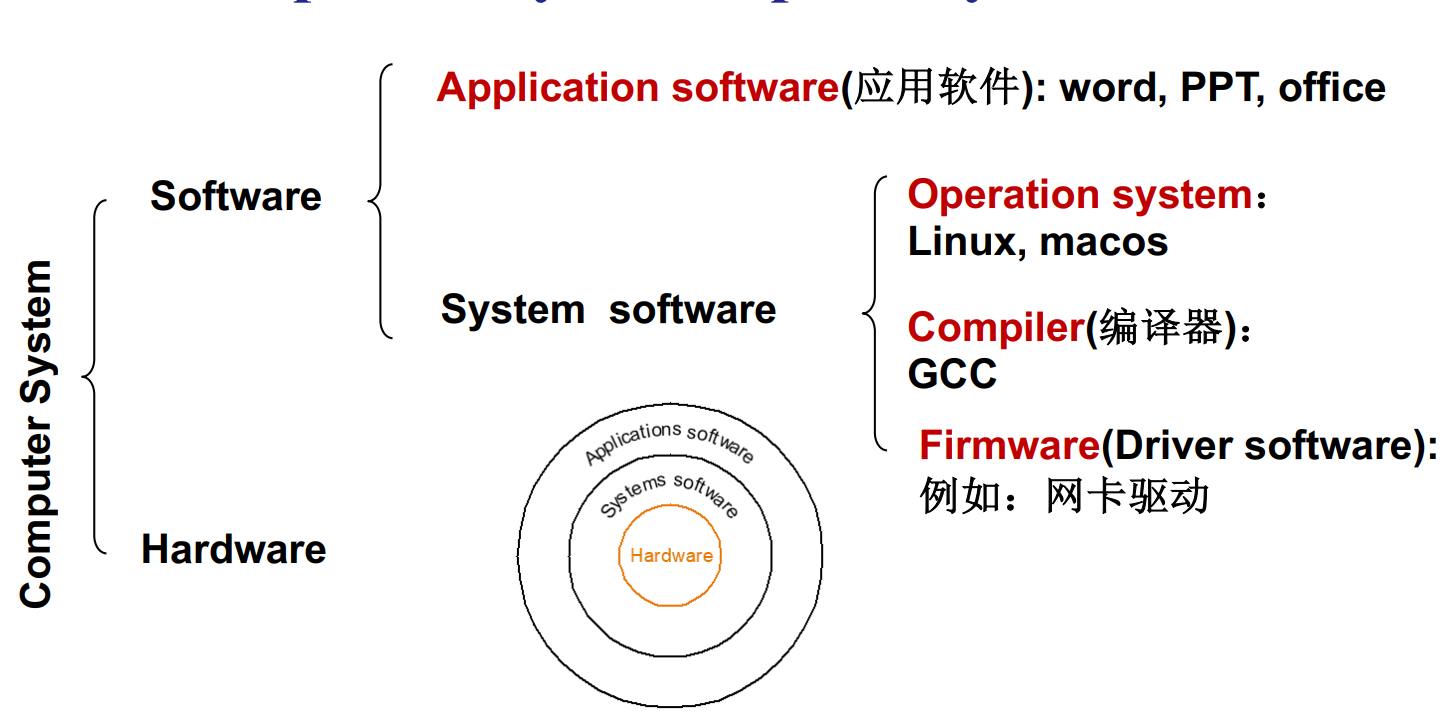
指令集(ISA)
-
ISA: The interface between hardware and lowest-level software.
指令集筑起了「硬件」与「软件」之间的桥梁。硬件生产厂商只需要支持指令集中的特定操作,而软件厂商只需要借助这些基本指令集来开发软件。
CPU Time Calculation
-
Basic Concepts
-
[CONCEPT] Response Time (Execution Time):响应时间,how long it takes to do a task.
-
[CONCEPT] Throughput (Bandwidth):吞吐率,total work done per unit time.
-
-
Performance Measurement
假设 X 比 Y 快 $n$ 倍,那么 $\frac{\text{Execution Time}_Y}{\text{Execution Time}_X}=n$。
-
Clock
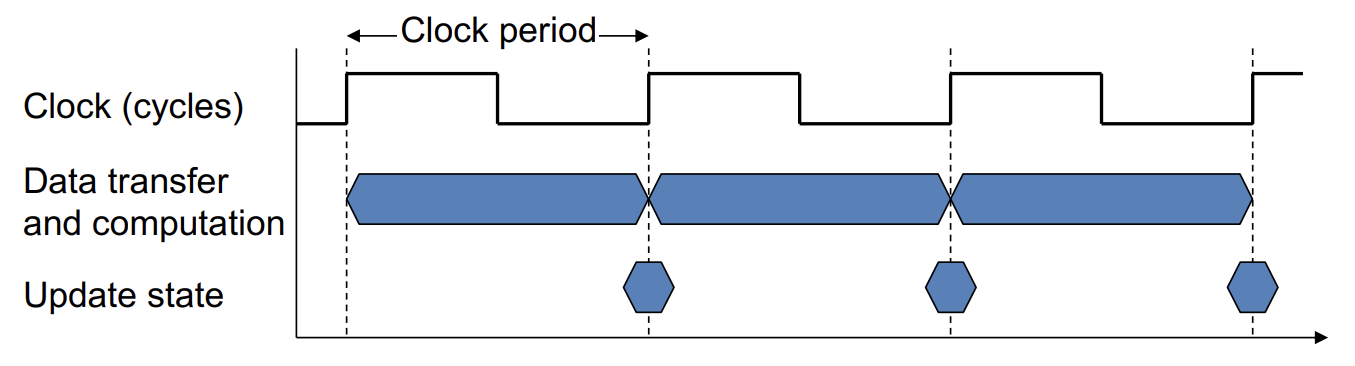
-
[CONCEPT] Clock Cycle Time: duration of a clock cycle.
-
[CONCEPT] Clock Rate: cycles per second,与 Clock period 成倒数。
-
CPU Time = CPU Clock Cycles × Clock Cycle Time = CPU Clock Cycles / Clock Rate
-
-
Considering Instructions
-
[CONCEPT] CPI: Cycles Per Instruction. CPI 的值由 CPU 本身决定,同时也受到指令种类的影响(例如,加法和乘法所需要的 Cycles 肯定不一样)。
-
Clock Cycles = Instruction Count × CPI
CPU Time = Instruction Count × CPI × Clock Cycle Time = Instruction Count × CPI / Clock Rate
-
考虑不同 Instruction Type 对 CPI 的影响……
$\text{Clock Cycles} = \sum\limits_{i=1}^n (\text{CPI}_i \times \text{Instruction Count}_i)$
加权平均 CPI(global CPI):字面意思。
-
-
Power Spent
$\text{Power} = \text{Capacitive load}^2 \times \text{Voltage} \times \text{Frequency}$
-
习题演示

Some Pitfalls / Fallacies
-
Amdahl’s Law 提升局部不一定能提升总体
\[T_{imporved} = \frac{T_{affected}}{\text{improvement factor}} + T_{unaffected}\]其中 $T_{imporved}$ 表示提升后的总用时。$\text{improvement factor}$ 表示受影响的提升方面的提升比例。此公式意在说明,对于某种提升,只有 affected 的部分会变快,unaffected 的部分怎么都不会变快。
例如,一个程序需要执行 80s 的乘法和 20s 的除法。无论乘法提升了多少,我们都无法把总时间提升 5 倍。
-
Low Power at Idle 功耗和负载不成正比
对于 i7 power benchmark,100% 负载下的功耗为 258W,50% 负载下为 170W,10% 负载下为 121W。也就是说,一味降低 CPU 的负载不一定能起到节能的效果。
-
MIPS as a Performance Metric? MIPS 是否能作为衡量 CPU 运行速度的参数?
MIPS: Millions of Instructions Per Second
\[\text{MIPS} = \frac{\text{Clock Rate}}{\text{CPI} \times 10^6}\]之前提及,CPI 除了受 CPU 本身的影响,也受到 CPI 种类等因素的影响。不同电脑的指令集架构不同,进而导致 CPI 不同;同时,不同指令的 CPI 也不一样。所以 MIPS 并非一个只和 CPU 本身有关的量。所以用 MIPS 来衡量 CPU 的运行速度是不合理的。
Eight Great Ideas
-
Design for Moore’s Law (设计紧跟摩尔定律)
-
Use Abstraction to Simplify Design (采用抽象简化设计)
-
Make the Common Case Fast (加速大概率事件)
-
Performance via Parallelism (通过并行提高性能)
-
Performance via Pipelining (通过流水线提高性能)
-
Performance via Prediction (通过预测提高性能)
-
Hierarchy of Memories (存储器层次)
-
Dependability via Redundancy (通过冗余提高可靠性)
-
Some illustrations:
Use Abstraction to Simplify Design:
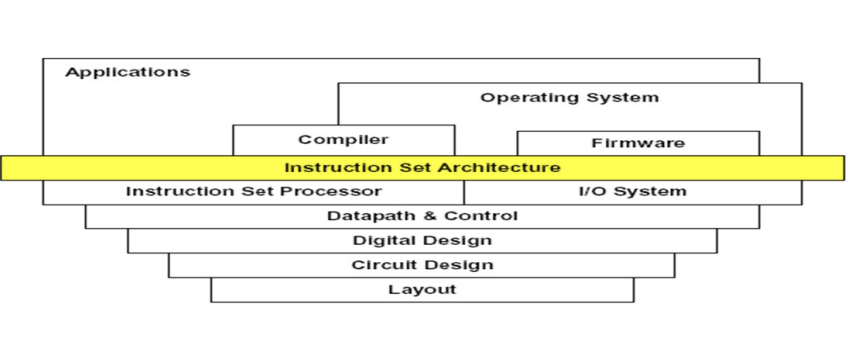
Performance via Pipelining:
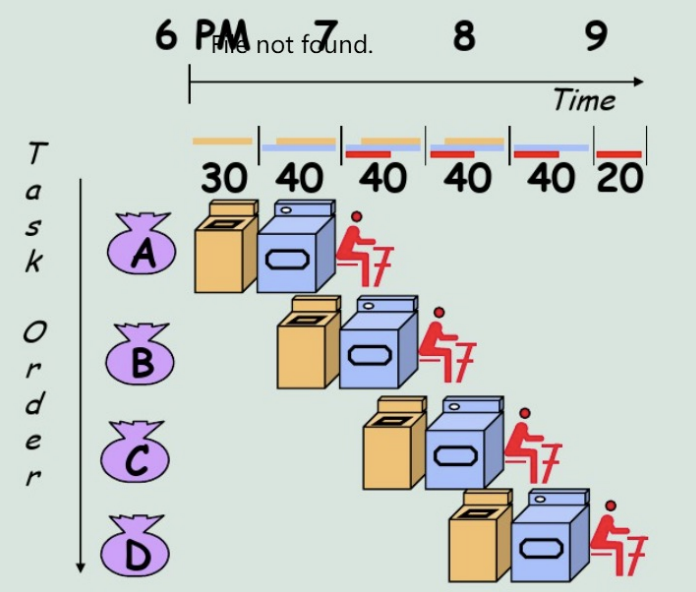
Chapter 3. Arithmetic for Computer
Signed Numbers Representations
| Binary | Signed Magnitude | 2’s Complement |
|---|---|---|
| 000 | +0 | +0 |
| 001 | +1 | +1 |
| 010 | +2 | +2 |
| 011 | +3 | +3 |
| 100 | -0 | -4 |
| 101 | -1 | -3 |
| 110 | -2 | -2 |
| 111 | -3 | -1 |
一般采取补码的表示方式。
Addition and Subtraction
减法可以改成加补码。这样加和减都统一成了加法。
加减法都可能产生 overflow。例如:
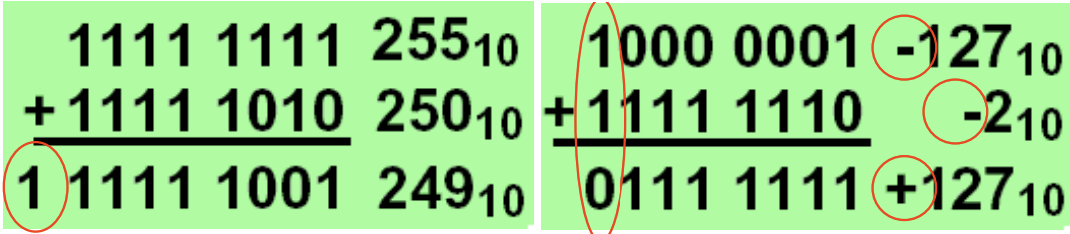
overflow 的判定遵循下表:
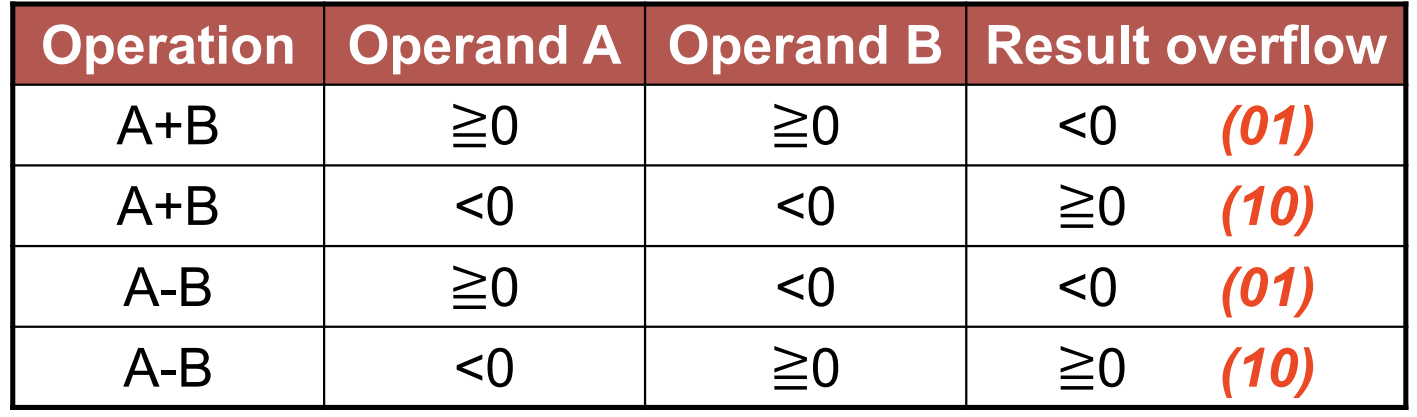
-
此处的 overflow 专指「溢出导致错误的计算结果」。例如 $(-1)+(-1)=(-2)$ 我们不认为发生了 overflow。
-
只有以上四种 A, B 组合才可能产生 overflow。例如一个正数加一个负数是不可能产生 overflow 的。
-
Result overflow 括号中的两个数分别表示「溢出位」和「最高位」。例如 $7+7=(0111)_2+(0111)_2=(1110)_2=-2$,其溢出位(第 4 位)为 $0$,最高位(第 3 位)为 $1$,属于表中的第一行情况。
-
可以看到「溢出位」和「最高位」在溢出情况下总是相反的,这意味着我们可以使用 XOR 门进行判定。
ALU
考虑建立具有如下功能的 ALU:
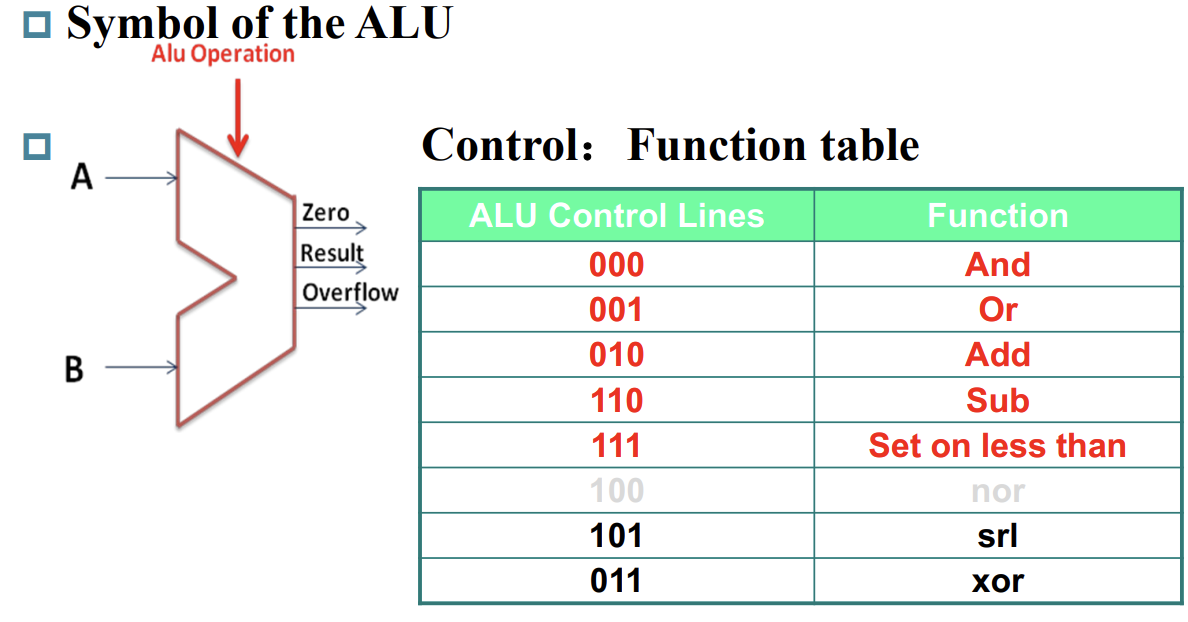
其中 srl 表示 shift right logical,Zero 位宽为 1,输出 1 当且仅当 Result 为 0。
-
And 与 Or
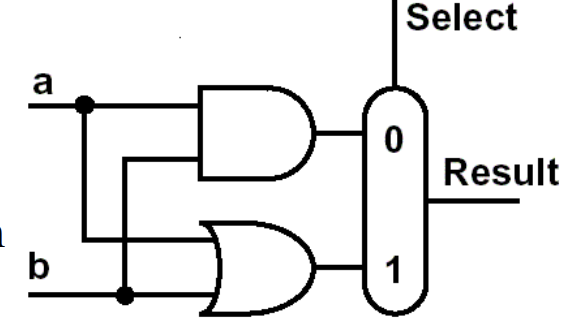
-
Add
全加器,$S=a \oplus b \oplus C_{in}, \ C_{out}=ab+aC_{in}+bC_{in}$。
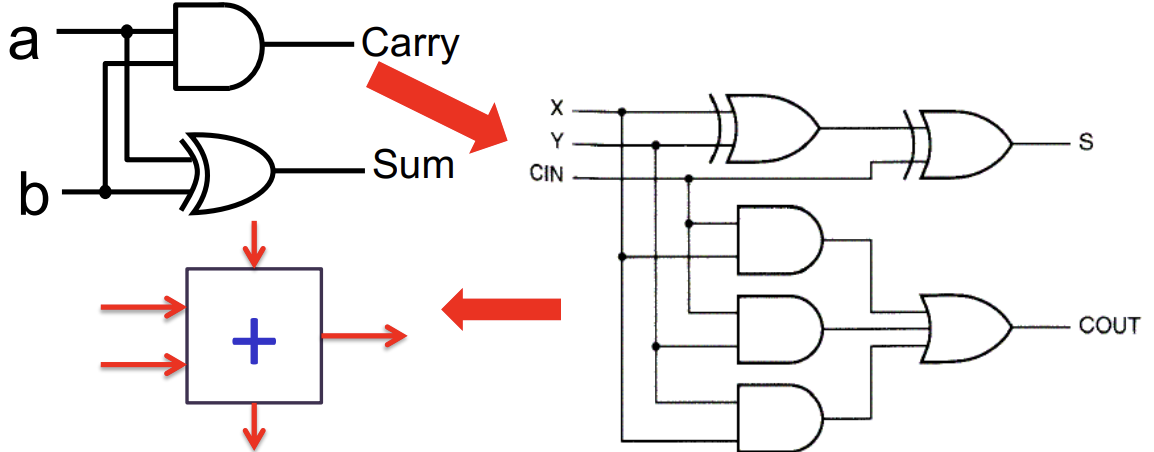
-
Sub
减法就是加上补码。考虑 And / Or / Add / Sub 的 ALU 设计如下:
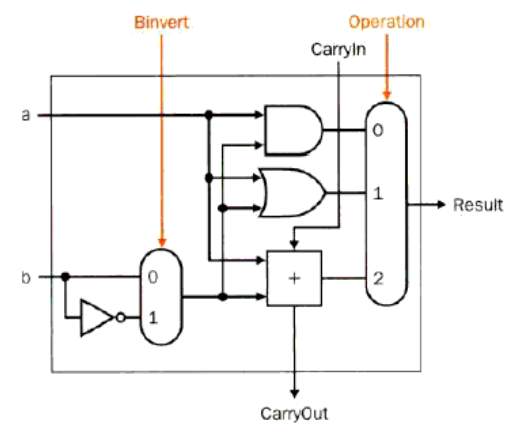
-
Set on less than (Comparison)
用于比较输入项 $a,b$ 的大小,如果 $a < b$,那么输出 $1$,反之输出 $0$。
实现方法是执行减法运算,看最高位(符号位)是否为 $1$ 即可。
考虑 And / Or / Add / Sub / Set on less than 的 ALU 设计如下:
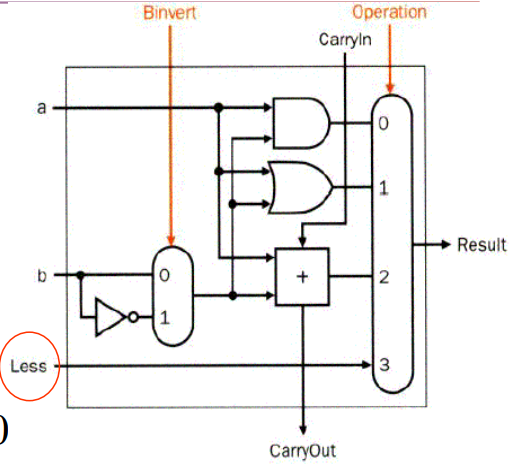
其中 MSB 的设计有略微不同(加入了溢出检测模块,输出 Set 和 Overflow 信号)
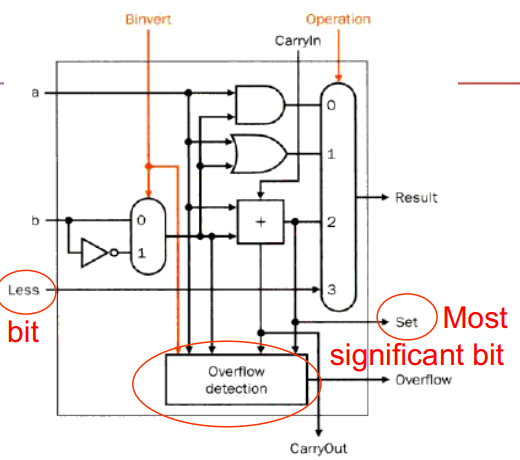
最后我们考虑建立整个 ALU。
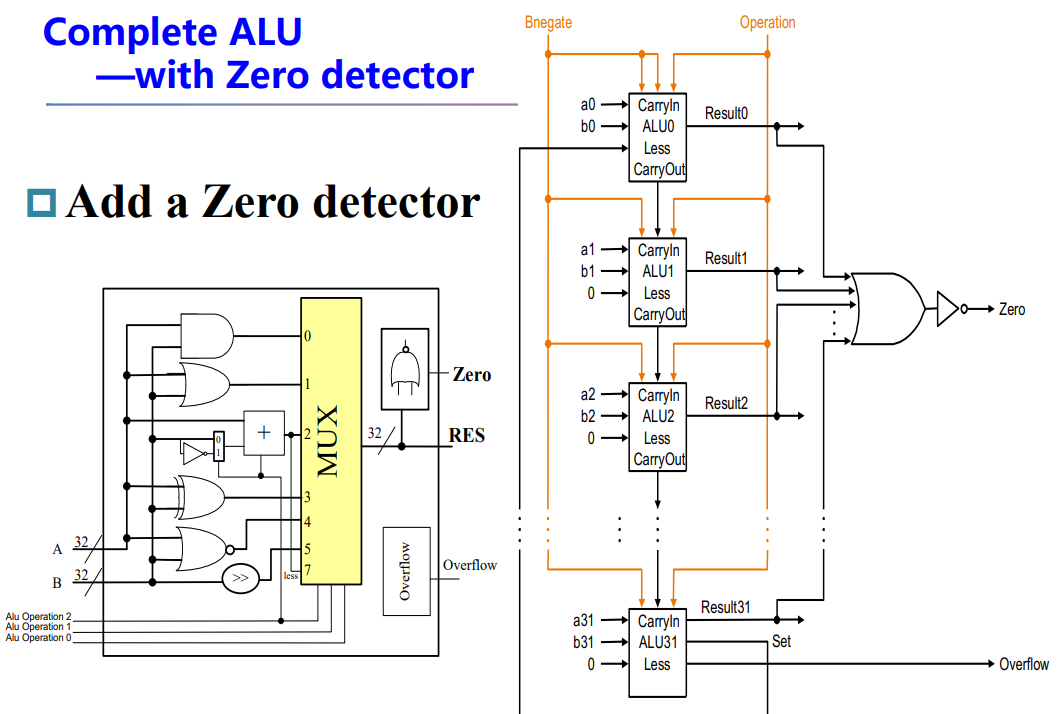
注意到 MSB 的 Set 连到了 LSB 的 Less 输入,用于执行 Comparison 运算;非 LSB 的 Less 输入均为零。
Fast Adder
Carry Lookahead Adder (CLA) 加速运算:本质上是把行波加法给「压缩」了。但受到 fan-in of gate 的影响,只有分组「压缩」。
此部分数逻已经学过,在此不再赘述。
Multiplication
名词:被乘数(multiplicand),乘数(multiplier),积(product)。
-
Multiplier Ver 1
Look at current bit position.
-
if multiplier is 1, then add multiplicand.
-
Otherwise add 0.
-
Shift multiplicand left by 1 bit.
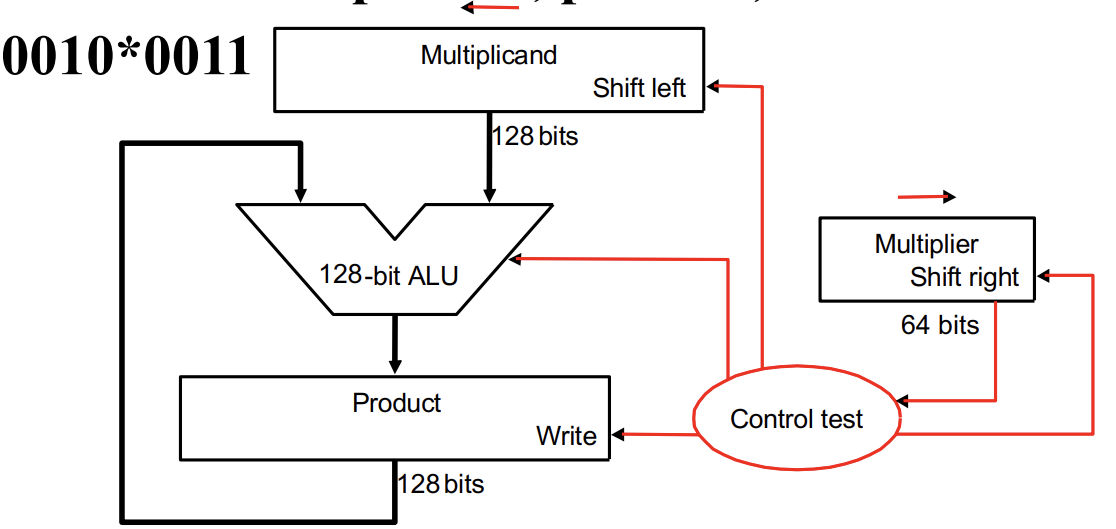
其实就是模拟的竖式乘法。对于两个 64 bits 的整数相乘,需要 128 bits 的寄存器存储积,同时也需要一个 128 bits 的 ALU 来执行加法。
-
-
Multiplier Ver 2
在第一版乘法器的基础上,第二版将「左移 multiplicand」改成了「右移 product」来减小 ALU 的开销。原理图和举例图如下。
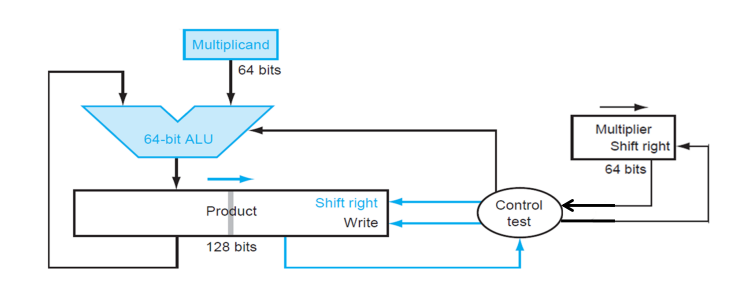
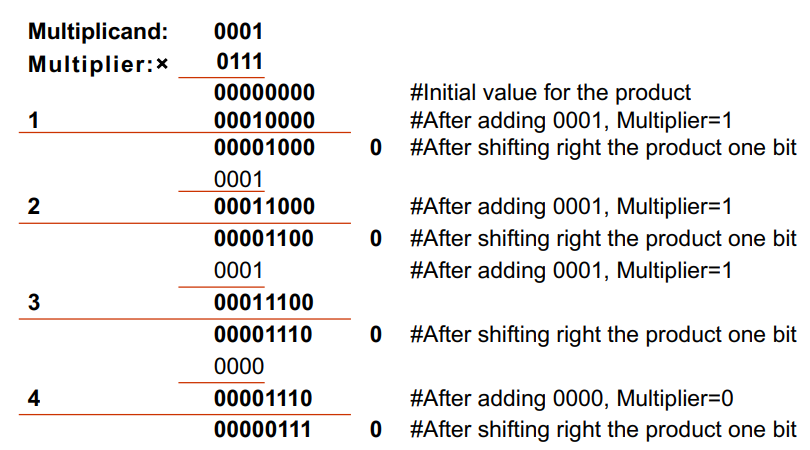
注意每一次是将 multiplicand 加到 product 左边的 64 位,而后进行不断的右移。对于两个 64 bits 的整数相乘,需要 128 bits 的寄存器存储积,但只需要一个 64 bits 的 ALU 来执行加法。
-
Multiplier Ver 3
基于第二版乘法器进行了一点小优化。回顾我们使用的 128 位的存储积的 reg,刚开始 reg 的右 64 位是空的,这意味着说我们可以将其用于存储 multiplier。并且随着后续 product 和 multiplier 的右移,两者也不会产生空间上的冲突。
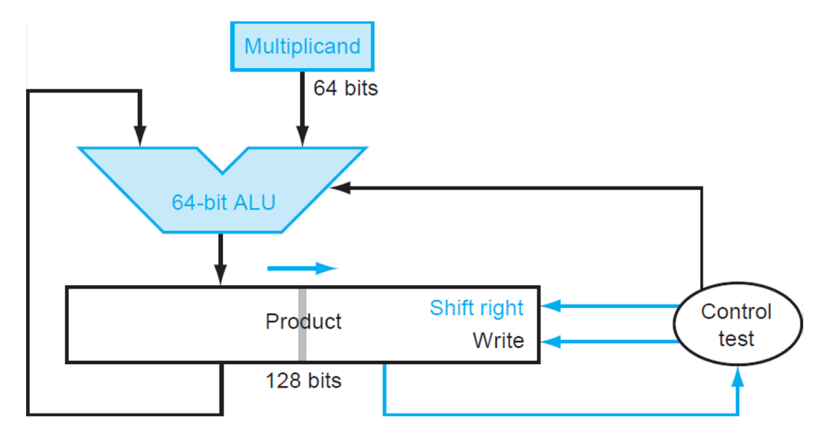
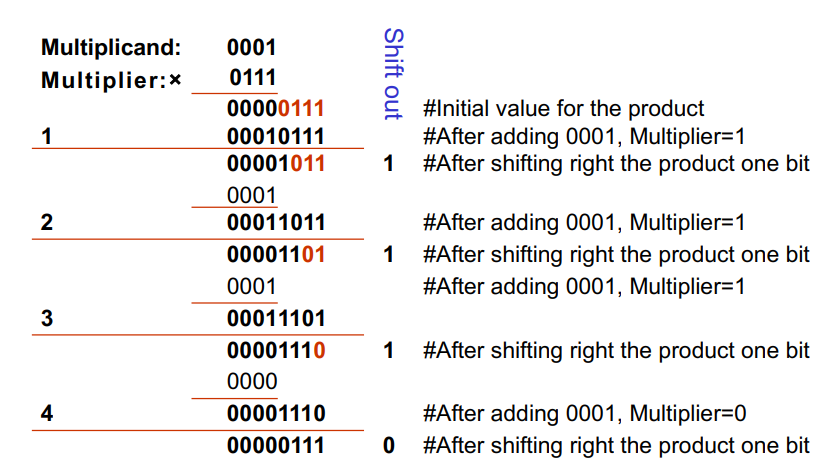
红色部分存储的是 multiplier。可以看到 multiplier 和 product 共用一个 reg。
-
有符号乘法
考虑有符号整数乘法。一种基本的方法是,符号和绝对值分开考虑。符号位直接进行 XOR,随后将 MSB 设为 0(去除符号位)并执行无符号乘法,最后将符号和绝对值的积合并即可。
此外还有一种方法:Booth’s Algorithm.
-
Booth 算法
Booth 算法的执行基于第三版乘法器,但是做了一定的优化。Booth 算法在加速了乘法的同时,也使得有符号的乘法运算更加统一(即不需要传统方法的分类讨论)。
考虑被乘数为 $y$,乘数为 $10111100$。按照第三版乘法器的做法,会执行 $8$ 次 shift 操作和 $5$ 次 add 操作。如果我们将 $10111100$ 改写为 $2^7+2^6-2^2$,则只需要执行 $8$ 次 shift 操作和 $3$ 次 add/sub 操作(在此我们假设 shift 速度快于 add/sub)。
-
流程
每次考察乘数的 0 位和 -1 位(此处 -1 位是人为补足的,初始为 0)。并按照以下表格执行操作:
bit(0) and bit(-1) Operations $10$ Subtract multiplicand from left half $11$ No arithmetic operations, just shift right $01$ Add multiplicand to left half $00$ No arithmetic operations, just shift right 此处依然是按照第三版乘法器那样将 product, multiplier 放在一起存储,且每次 shift right 都是将两者一起右移。
同时:每次右移最高位的不足不再是无脑补零,而是和原最高位一样补(即每次右移保持符号位不变)。
-
例子
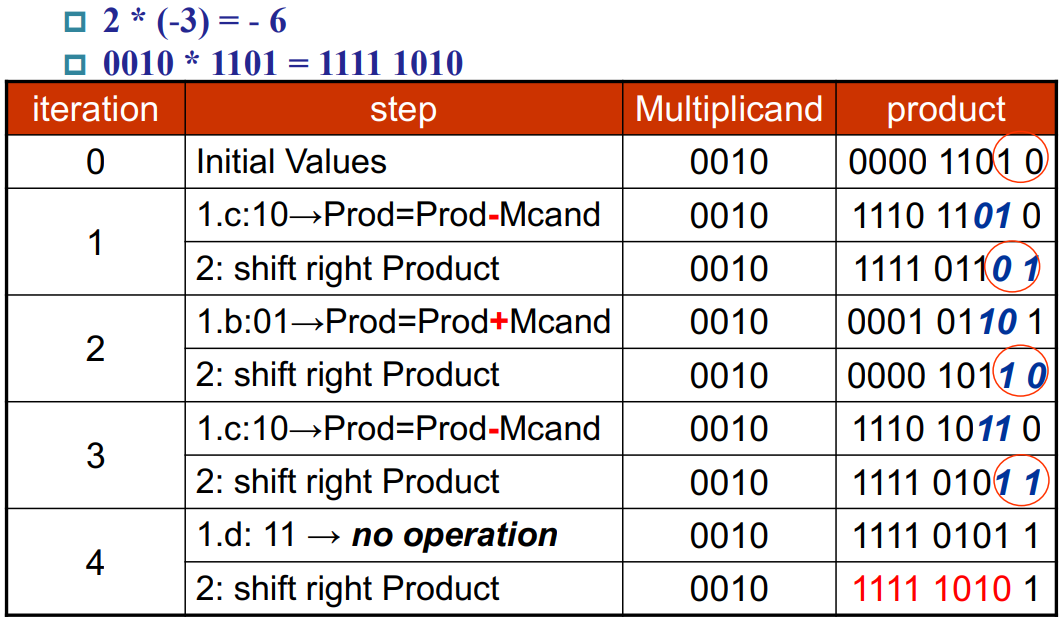
注意执行的轮次数和乘数的 bit 数一致。第一轮是 10,第二轮是 01,第三轮是 10,第四轮是 11,第五轮(本来是 11)无需执行。
-
一些粗浅的理解
关于加减法: 遇 10 则减,遇 01 则加其实比较好颅内理解。00 和 11 不干事都是为了「把锅甩给后面的高位」。
关于右移最高位补足、为何不进行第 5 轮: 首先考虑另外一个问题,为什么常规无符号乘法无法做有符号的乘法。例如,$0010 \times 1101 = 00011010$,正负得正,显然是有问题的。
实际上问题出在位数不足。补齐后 $00000010 \times 11111101 = 11111010$ (取低 8 位)就没有问题了。
然而把四位乘法转化为 8 bits × 8 bits 做是有点亏的,同时注意到有很多连续的 1 似乎加法也会很多。所以使用 Booth’s Algorithm。
解答这个问题可能需要考虑 8 bits × 8 bits 的本原做法。比如在 iteration 1 中要减去被乘数,在算法中体现的是 +1110,然而实际上应该是 +11111110。这样在整体右移一位之后最高位确实应该为 1。
为何不进行最后一轮似乎也和这个有关。像比如上图的例子,按理说最后应该再做一个 left half 的 +0010 才对,然而当我们把乘数 $1101$ 补全为 $1111 \ 1101$ 后,发现实际上这个 +0010 应该在 iter 9 执行,实际上表现出来的就是溢出了 8 bits 的范围。
-
Division
名词:被除数(dividend),除数(divisor),商(quotient),余数(remainder)。
-
Division Introduction
-
除数为 0 一般交由软件判断。
-
有符号除法一般将符号和绝对值分开讨论。
-
-
Division Ver 1
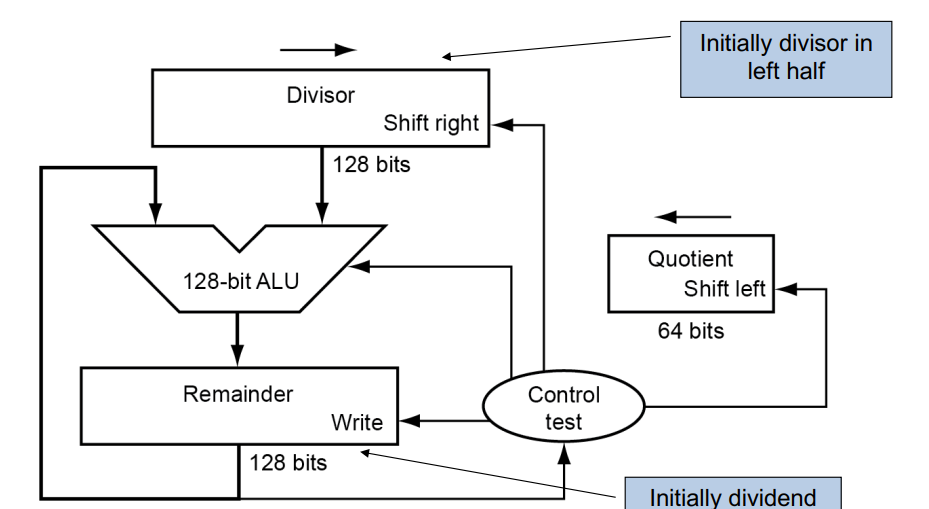
假设 dividend 和 divisor 都是 64 位的。
-
首先将实际的 divisor 放到高 64 位(低 64 位为零)。remainder 初始设置为 dividend。
-
接下来每次拿 remainder 减去 divisor。若减后 remainder 大于等于 0,则将 quotient 左移并将 LSB 设为 1;若减后 remainder 小于 0,则恢复原值(把 divisor 加回去),同时也将 quotient 左移。
-
将 divisor 右移一位。重复 65 次。
其实就是模拟的竖式除法。一个示例如下。
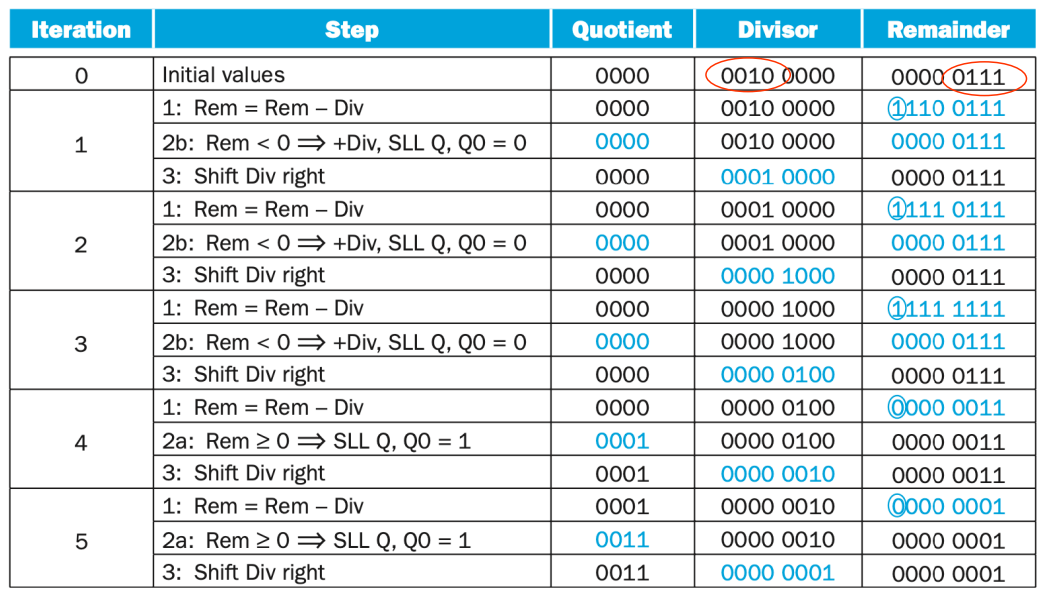
-
-
Division Ver 3
和之前的 Multiplier V3 一致的思路:将 remainder 和 quotient 放在一个 reg 中存放。
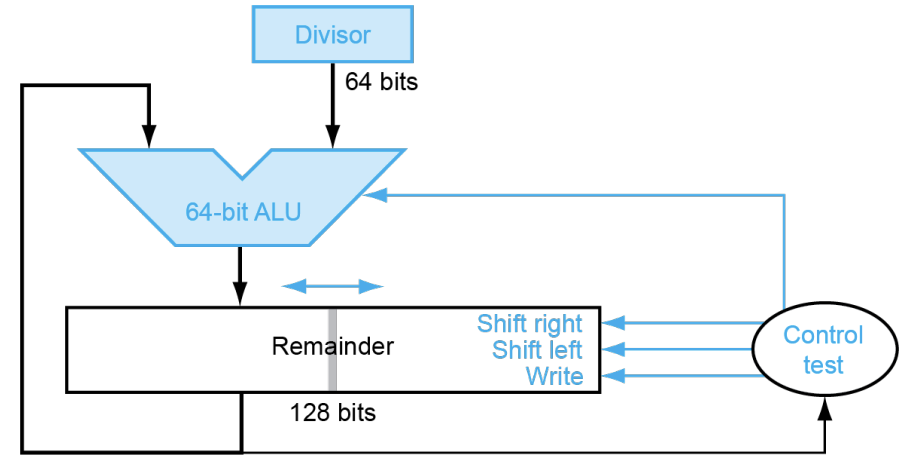
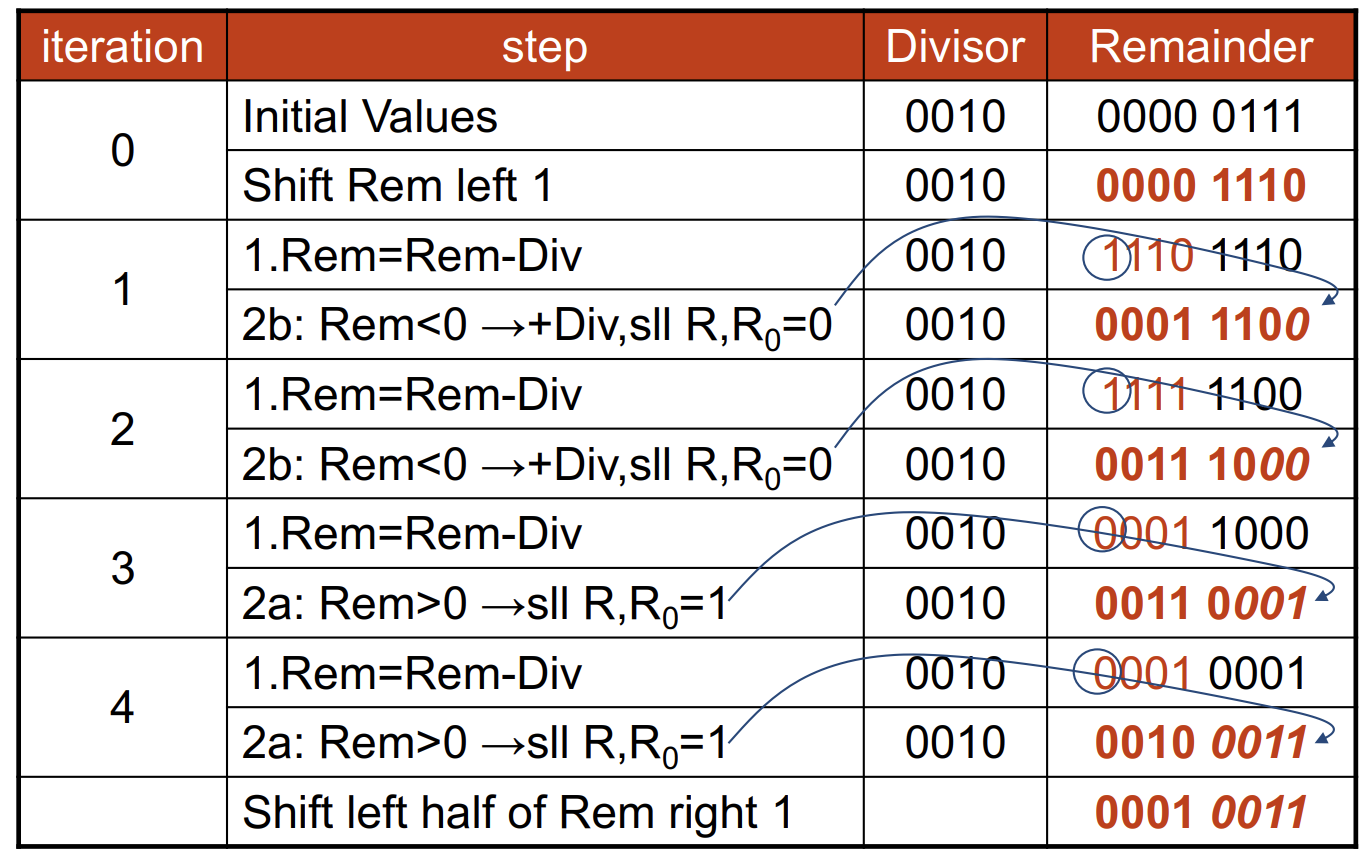
注意初始的时候就可以将 remainder 左移一位(对应 iter0,因为第一次必然失败)。最后 reg 中的 left half 即为 remainder,right half 即为 quotient。
Float
-
浮点数的存储与定义
浮点数的存储分为三部分。
- float:符号位 $S$ (1bit),指数位 $E$ (8bits),系数位 $F$ (23bits)。
- double:符号位 $S$ (1bit),指数位 $E$ (11bits),系数位 $F$ (52bits)。
其意义为二进制下的科学计数法表示:$(-1)^S \times 1.F \times 2^{E+bias}$。
实际使用时指数位 $E$ 会有偏差 $bias$,这是为了处理 $E$ 可能为负的情况。对于 float,$E$ 存储值比实际值大 $bias=127$;对于 double,$E$ 存储值比实际值大 $bias=1023$。
特别规定:
- 当 $E=111…11, \ F=000…00$,表示此浮点数为无穷。
- 当 $E=111…11, \ F \neq 000…00$,表示此浮点数为 NaN。
-
浮点数加法
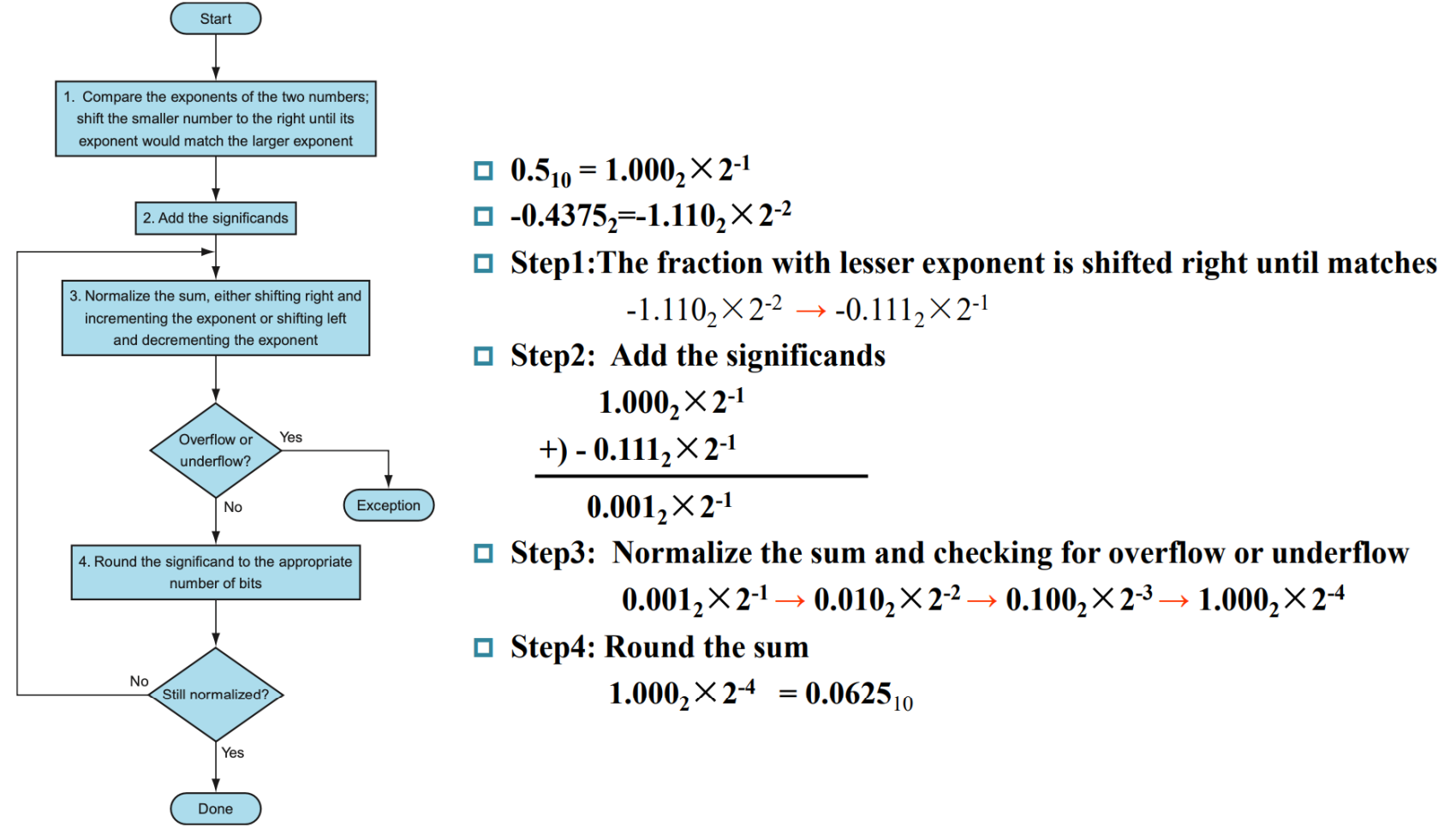
算法流程与示例:
-
比较两数的指数位,确定大小关系并把指数位较小的通过 $F$ 右移(小数点则向左移动)使得两操作数的指数位 $E$ 一致。
-
将 $F$ 相加。
-
归一化(比如加法之后产生了进位,那么 $E$ 应当加一,$F$ 则右移)。
-
Rounding(比如四舍五入)
-
再次归一化(例如 9.99 round 后变为 10.00,此时需要再次归一化,当然这只是一个十进制的例子)
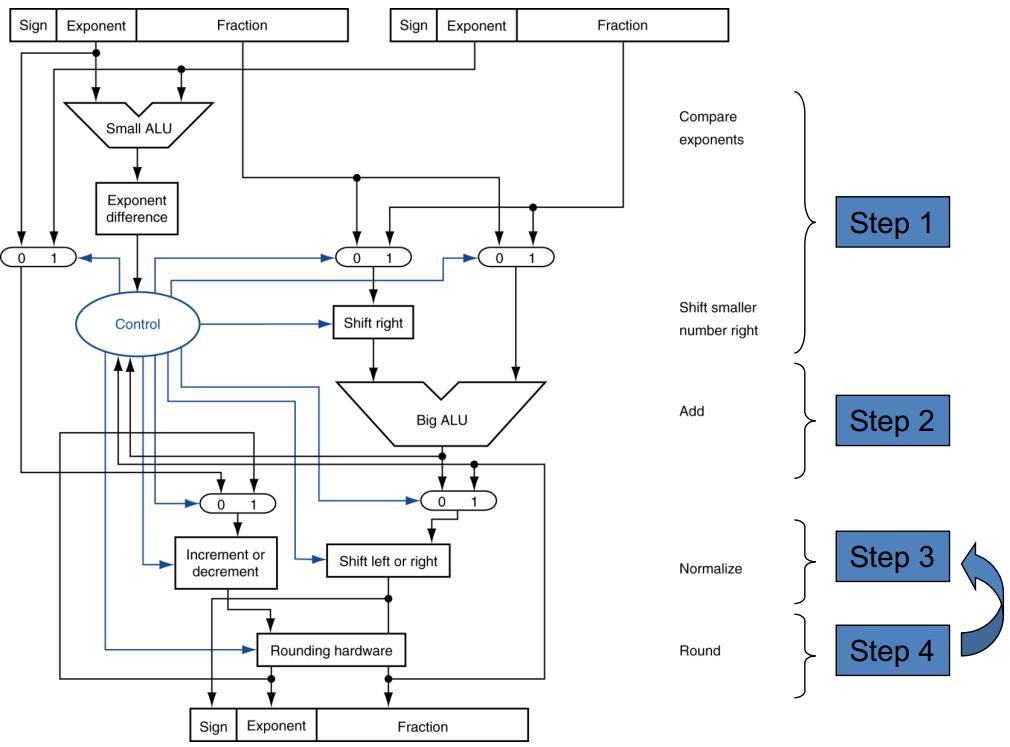
逻辑结构图绘制:
-
-
浮点数乘法
区别主要集中在:
- 符号位单独处理
- 指数位 $E$ 相加后要减去对应的 $bias$。
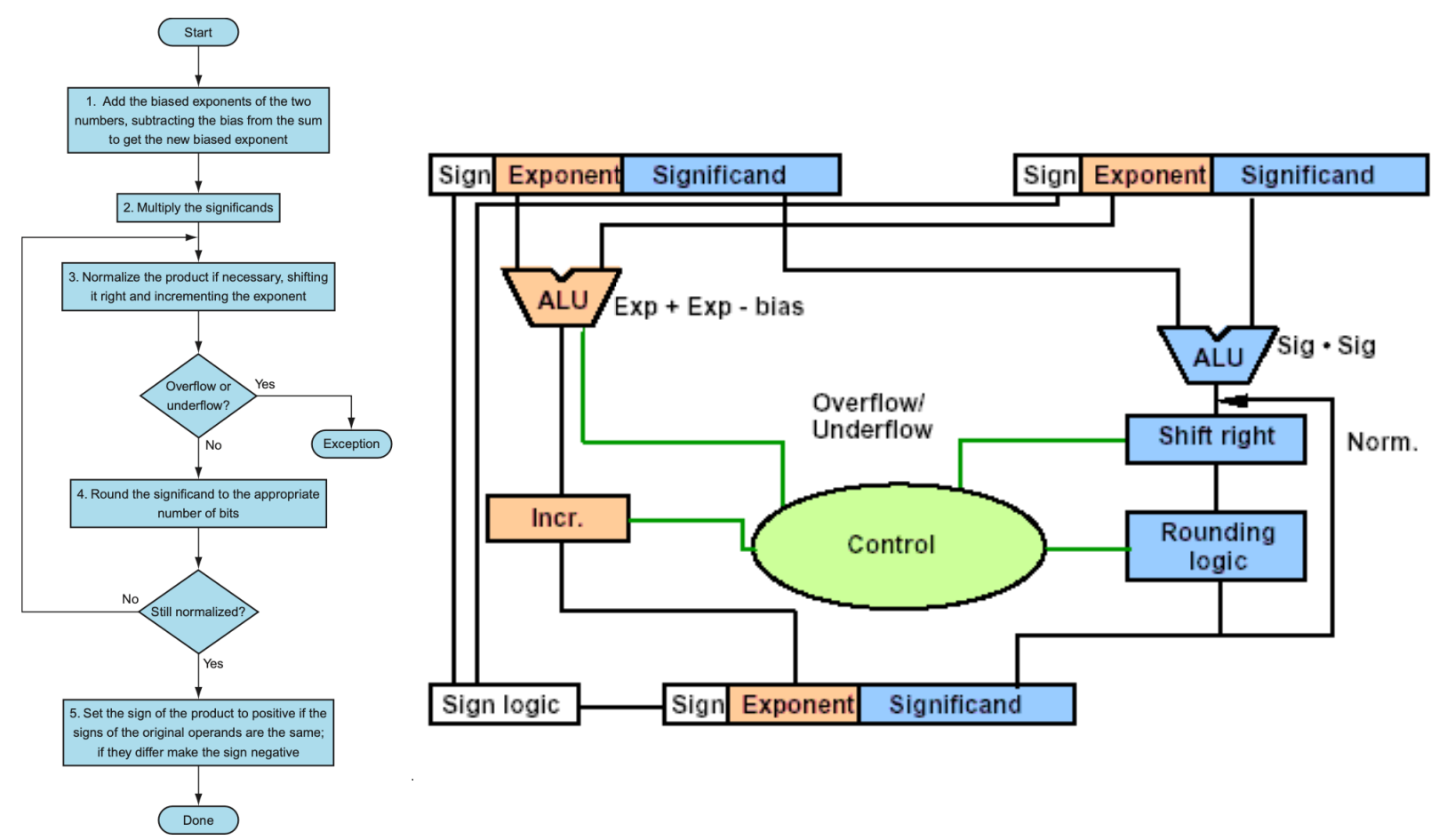
-
Accurate Arithmetic 浮点数精度问题
一些术语:
-
保留位 (guard bit):第一个被舍掉的位。
-
近似位 (round bit):guard bit 的后面一位,亦即第二个被舍掉的位。
-
粘滞位 (sticky bit):round bit 后面的所有位的 OR 构成 sticky bit。
Rounding 规则如下:

-
Enjoy Reading This Article?
Here are some more articles you might like to read next: